كثيرا نسمع عن الديسبل في الهندسة الصوتية. ولكن هناك مفاهيم ملتيسة لدى البعض عن الديسل. سنحاول في هذه المقالة أن نبسط مفهوم الديسبل بشكل رياضي وكيف واين يتم استخدامه
اللوغاريتم والديسبل
ان دراسة علم الصوت تتطلب معرفة جيدة باللوغاريتم ومعادلاته واستخداماته, وكذلك الديسبل الذي يعتبر واحدة القياس الرئيسية للكثير من التعاريف والمحددات الصوتية. لذلك سنتطرق في هذه الفقرة الى مراجعة بسيطة للوغاريتم والديسبل حتى ندرك كيف يتم استخدامها في علم الصوت.
اللوغاريتم Logarithm
لنأخذ أولا المعادلة التالية:
y = bx
الان اذا فرضنا أن قيمة b= 10. تصبح المعادلة السابقة كما يلي:
y = 10x
الان لو اردنا ان نستخرج قيمة (x) من هذه المعادلة فتكون هي لوغاريتم (y) للأساس 10 وتكتب بالشكل التالي:
Log10(y) = x
عادة الاساس العشري لايكتب لذا تكتب المعادلة السابقة كما يلي:
Log y = x
طبعا قيمة b يمكن أن تكون اي عدد طبيعي ويكون اللوغاريتم اساسه هذا الرقم, فإذا كانت قيمة b هي6 فإننا نقول لوغاريتم العدد y للاساس 6.
ولكننا افترضنا ان قيمة b id الرقم (10) لأنه الوغاريتم ذو الاساس (10) هو المستخدم في علم الصوت.
لوفرضنا أن قيمة y=10 , فإن قيمة x تكون:
x= log 10 = 1
(اي لوغاريتم 10 للاساس 10هو واحد).
ولو أن قيمة y=1 , فإن قيمة x تكون:
x= log 1 = 0
(اي لوغاريم الواحد هو صفر).
ولو أن قيمة y=1000000 , اي مليون. فإن قيمة x تكون:
6= x= log 106
اي ان لوغاريتم المليون هو (6).
ومن هنا تنبع أهمية اللوغاريتم من ناحية استخدام ارقام ذات قيمة صغيرة للتعبير عن قيم معينة كبيرة حيث نجد أن بعض القيم الصوتية يكون مجالها واسع جداً واستخدام اللوغاريتم للتعبير عنها يبقي هذا المجال ضيقاُ قليلاً.
الديسبل Decible
يعتبر الديسبل decibele ويرمز له dB من أهم الواحدات في علم الصوت. ويستخدم كواحدة لعدة قيم في الصوت وأهمها قياس شدة الصوت أو مستوى الصوت sound pressure level. اضافة الى استخداماته في عديد من مجالات الهندسة الالكترونية والاتصالات وغيرها.
الديسبل بشكل عام هو التعبير اللوغاريتمي (للاساس العشري) للنسبة بين قيمتين معينتين, مثل الاستطاعة أو الجهد الكهربائي أو شدة الصوت أو غيرها. ويأخذ العلاقة التالية:
10Log A1/A2
حيث A1 و A2 هي أحد القيم المذكورة أعلاه.
فرضاُ لدينا سماعتين (تعملان على نفس التردد وضمن نفس المحيط), الاولى تعطي قدرة أو استطاعة P1, والثانية قدرتها P2, الفرق بين قدرة السماعتين بالديسبل يحسب بالمعادلة التالية:
10Log P1/P2
الان اذا فرضنا أن السماعة الاولى قدرتها 50 واط. والثانية 100 واط, أي السماعة الثانية قدرتها ضعف الاولى. يكون الفرق بين السماعتين هو فقط 3 ديسبل.
log (P2/P1) = 10 log 2 = 3 dB.
اذا السماعة الثانية قدرتها عشرة أضعاف السماعة الاولى, الفرق بينهما يكون:
10Log10= 10 dB
اما اذا كانت قدرة السماعة الثانية أكبر من السماعة الاولى بمليون مرة فإن الفرق بين السماعتين هو (60dB) كما مبين بالغلاقة التالية:
10Log 1000000= 10×6= 60dB
لا حظ هنا كيف تم التعبير عن نسبة الفرق بين قدرتي السماعتين بأرقام مبسطة أكثر.
قياس شدة الصوت باللوغاريتم.
اذا اردنا ان نعطي للصوت قيمة رياضية يتم التعامل مها بالارقام فلا بد من أساس نرتكز عليه لدى تعريفنا لقوة الصوت, بمعنى اذا اردنا أن نقارن بين صوتي سماعتين لنبين من هي الاقوى لابد من تعريف للصوت الاقوى بشكل رياضي.
و تم اختراع ما يسمى (شدة ضغط الصوت) أو (sound pressure level) وتسمى اختصارا (SPL). ويقاس بواحدة الضغط وهو الباسكال Pa.
تم قياس أقل مستوى صوت يمكن أن تسمعه الاذن البشرية ووجد أنه 20 ميكرو باسكال. 20micropascal.
وهذه القيمة هي المرجع الذي يتم بناء عليه قياس شدة الصوت وتسمى (عتبة سماع الصوت) او (Threshold of Hearing).
اي أن تكون p1 في التعبير الرياضي السابق هو قيمة أقل صوت تسمعه الاذن البشرية. وعلى اساسه يتم يقاس باقي الاصوات من حيث قوتها.
وعلى هذا الافتراض فإن مستوى أقل صوت تسمعه الاذن البشرية هو (0) ديسبل.
يتراوح المجال الذي تسمعه الاذن ما بين أخفض مسوى وهو 0dB و اعلى مستوى والذي يكون 120 dB.
أعلى مستوى يدعى (عتبة الألم) او pain threshold وهو حوالي 60 Pa حيث ان الاذن لدى سماع صوت والذي يقدر بمستوى 120 ديسبل تعطي احساس بالالم. طبعاُ الصوت الذي هو أعلى من هذه الدرجة يسبب أذى في الأذن يصل الى حد (الطرش).
صوت المحادثة الطبيعية بين شخصين هو حوالي 70 dB.
التغيير في مستوى شدة الصوت ل (1) ديسبل هو أقل تغيير يمكن للأذن البشرية ملاحظته.
ملاحظه هامة:
التغيير الذي يتم ادراكه من قبل الاذن على أنه حصل تغيير محسوس في مستوى الصوت هو 3dB
بينما التغيير بقيمة 10 dB. تدركه الاذن وكأن الصوت قد تم مضاعفته.
لدى حساب مستوى شدة الصوت بالدسبل نستخدم العلاقة التالية:
SPL(dB) = 20 Log P/Pref
حيث P هي ضغط الصوت بالباسكال. و Pref هو ضغط أقل صوت تصمعه الاذن البشرية المذكور أعلاه.
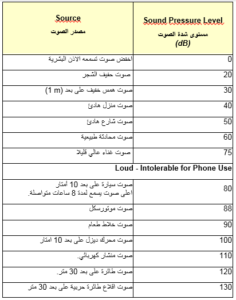
الجدول التالي يبن مستوى شدة الصوت لعدة مصادر صوتية تعطيك فكرة عامة عن مستويات الاصوات.
ملاحظة
أن قيمة صفر ديسبل( 0 dB ) لاتعني انه لايوجد صوت مطلقاً, ولكن تعني أن مستوى الصوت الذي يتم قياسه هو يساوي تماماً مستوى أقل صوت تسمعه الاذت البشرية, والذي هو المرجع الذي يتم حساب مسوي الصوت غلى اساسه, اي preference والذي ذكرنا سابقا أنه يساوي 20 ميكروباسكال او 20miropascal.
وهذا ما تستنتجه من العلاقة:
sound level = 20 log (pmeasured/preference) = 20 log 1 = 0 dB
هل هناك صوت قيمته سالب؟
نعم يوجد صوت قيمته سالبة, وذلك اذا كان هذا الصوت أقل من المستوى المرجعي المعتمد. حيث أن لوعاريتم الاغداد السالبة هي أقل من الصفر.
فإذا قلت أن صوت شدته 20dB- فهذا يعني أن شدة هذا الصوت هي أقل بعشر مرات من شدة الصوت المرجعي.
جهاز قياس الديسبل Decibel meter
هناك العديد من الأجهزة المنتشرة في الأسواق والتي تمكن من قياس مستوى الصوت في والتي تسمى Sound Level Meter, اسعارها متفاوتة بشكل كبير. طبعاٌ فرق السعر سيكون على حسب دقة الجهاز.
كما أن هناك العديد من التطبيقات التي يمكن تحميلها على الجوال والتي تعطي قياس مستوى الصوت. ولكن هذه التطبيقات والاجهزة الرخيصة لا يتم الاعتماد عليها في الانظمة الاحترافية والتي تتطلب على الاقل وجود مكرفون ذو مواصفات عالية وهذا ما لاتوفره هذه الاجهزة.
عي كل حال سنوفر في المستقبل مقالة خاصة غن أجهزة قياس شدة الصوت. ولكن حالياً سنعطي فكرة عامة عن ميزة يجب أن تحويها هذه الاجهزة وهي فلتر يدعى “A weighting filter”
قبل أن نشرح ما هو هذا الفلتر, لابد أولاً أن نعرف أن الاذن البشرية لاتستجيب الى كافة الترددات بنفس الشدة. بمعنى أن (علو) الصوت لا تستجيب له الاذن بنفس الشكل لكل الترددات, حيث أن الاذن البشرية تستجيب للترددات في المجال 1000-4000 Hz أكثر من أي ترددات أخرى. لهذا يتم اضافة الفلتر المذكور أعلاه حتى تكون استجابة جهاز قياس شدة الصوت مماثلة للاذن البشرية. وتكون واجدة القياس المتبعة بعد اضافة هذا الفلتر هي dBA.
هناك ايضا فلاتر أخرى تضاف الى هذا الجهاز ولكن لامجال لشرحها الان.
استعمال الديسبل كواحدة قياس الجهد
قلنا سابقا أن الديسبل هو تغبير لوغاريتمي للنسبة بين قيمتين مثل الاستطاعة او شدة الصوت أو الجهد الكهربائي.
فإذ أخذنا الاستطاعة فإن التعبير اللغاريتمي
10 log P2 /P1
اذا اردنا التحويل الى الجهد الكهربائي وحيث أن علاقة الجهد بالاستطاغة او القدرة id
P=V2.R
وبما أن المقاومة R لا تتغير وأذا بدلنا قيمة P ب قيمة V في الغلاقة السابقة واختصرنا R
10 Log P2/P1= 10 Log V22/V21= 10 Log(V 2/ V1)2 = 20 Log V2/V1
أي أن التعبير اللوغاريتمي للجهد الكهربائي هو:
dB (V)= 20 Log V2/V1
الان لو فرضنا أن قيمة الجهد المرجعي هو (1) فولت. يكون تعبير الفولت بالديسبل هو:
dBv = 20 Log V
اما لو فرضنا أن قيمة الجهد المرجعي هو (0.775) فولت اي القيمة الاسمية. يكون تعبير الفولت بالديسبل هو:
dBu = 20 Log V
حيث يتم استخدام الحرف u بدلا من الحرف v.
[wd_contact_form id=”1″]